Suffix trees

Suffix trees are an application to particularly fast implement many important string operations like searching for a pattern or finding the longest common substring.

Introduction and definitions

I already introduced the Z-Algorithm which optimizes the searching for a pattern by preprocessing the pattern. It is very useful if you have to search for one single pattern in a large number of words. But often you’ll try to find many patterns in a single text. So the preprocessing of each pattern is ineffective. Suffix trees come up with a preprocessing of the text, to speed up the search for any pattern.

As expected a suffix tree of the word \(S\in\Sigma^+\) (length \(|S|=m\)) is represented in a data structure of a rooted tree. Every path from root to a leave represents a suffix of \(S\\)$ with \(\$\notin\Sigma\). The union \(\Sigma\cup\$=\tilde{\Sigma}\). Every inner node (except root) has at least two children. Every edge is labeled with a string of \(\tilde{\Sigma}^+\), labels of leaving edges at a single node start with different symbols and each leaf is indexed with \(1\dots m\). The concatenation of all edge labels on a path from root to a leaf with index \(i\) represents the suffix \(S[i\dots m]\).

Definition 1: For each node \(n\):

The path from root to \(n\) is called \(p\)

• The union of the labels at all edges on \(p\) is \(\alpha\in\tilde{\Sigma}^*\)
• \(\alpha\) is label of path \(p\) (\(\alpha=\text{label}(p)\))
• \(\alpha\) is path label to \(n\) (\(\alpha=\text{pathlabel}(n)\))
• instead of \(n\) we can call this node \(\overline \alpha\)

Definition 2: A pattern \(\alpha\in\Sigma^*\) exists in suffix tree of \(S\in\Sigma^+\) (further called \(ST(S)\)) if and only if there is a \(\beta\in\tilde{\Sigma}^*\), so that \(ST(S)\) contains a node \(n\) with \(\alpha\beta=\text{pathlabel}(n)\) (\(n=\overline{\alpha\beta}\)).

Definition 3: A substring \(\alpha\) ends in node \(\overline \alpha\) or in an edge to \(\overline{\alpha\beta}\) with \(\beta\in\tilde{\Sigma}^*\).

Definition 4: A edge to a leaf is called leaf-edge.

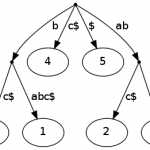
The tree \(ST(ababc)\) contains all suffixes of the word \(ababc\) extended with \(\\)$. This tree is visualized in figure 1.

Building suffix trees: Write only top down

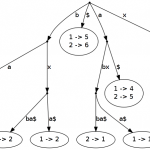
The write-only, top-down (WOTD) algorithm constructs the suffix tree in a top-down fashion.

Algorithm

Let \(\overline \alpha\) be a node in \(ST(S)\), then \(\alpha\) denotes the concatenation of all edge labels on the path to \(\overline \alpha\) (\(\alpha=\text{pathlabel}(\overline \alpha)\)). Each node \(\overline \alpha\) in the suffix tree represents the set of all suffixes that have the prefix \(\alpha\). So the set of pathlabels to leafs below \(\overline \alpha\) can be written as \(R(\overline \alpha)=\{\beta|\beta \in \tilde{\Sigma}^* \wedge \alpha\beta \text{ is suffix of }S\}\) (all suffixes of the set of suffixes that start with \(\alpha\)).

This set is splitted in equivalence classes for each symbol \(c\) with \(G(\overline \alpha, c)=\{c\beta\|c\in \tilde{\Sigma}\wedge c\beta \in R(\overline \alpha)\}\) is the \(c\)-group of \(R(\overline \alpha)\).

Case 1: For groups \(G(\overline \alpha, c)\) that contain only one suffix \(\beta\) we create a leaf \(\overline{\alpha\beta}\) with the index \(|S| - |\alpha\beta|\) and connect it to \(\overline \alpha\) with an edge containing label \(\beta\). Case 2: In groups \(G(\overline \alpha, c)\) with a size of at least two we compute their longest common prefix \(\gamma\) that starts with \(c\) and create a node \(\overline{\alpha\gamma}\). The connecting edge between \(\overline \alpha\) and \(\overline{\alpha\gamma}\) gets the label \(\gamma\) and we continue recursively with this algorithm in node \(\overline{\alpha\gamma}\) with \(R(\overline{\alpha\gamma})=\{\beta|\beta \in \tilde{\Sigma}^* \wedge \alpha\gamma\beta \text{ is suffix of }S\}=\{\beta|\gamma\beta\in R(\overline \alpha)\}\)

Applications

Exact pattern matching

All paths from the root of the suffix tree are labeled with the prefixes of path labels. That is, they’re labeled with prefixes of suffixes of the string \(S\). Or, in other words, they’re labeled with substrings of \(S\). To search for a pattern \(\delta\) in \(S\), just go through \(ST(S)\), following paths labeled by the characters of \(\delta\). At any node \(\overline\alpha\) with \(\alpha\) is prefix of \(\delta\) find the edge with label \(\beta\) that starts with symbol \(\delta[|\alpha|+1]\). If such an edge doesn’t exists, \(\delta\) isn’t a substring of \(S\). Otherwise try to match the pattern with \(\beta\) to node \(\overline{\alpha\beta}\). If \(\alpha\beta\) is not a prefix of \(\delta\) you’ll either get a mismatch denoting that \(\delta\) isn’t a substring of \(S\), or you ran out of caracters of \(\delta\) and found it in the tree. If \(\alpha\beta\) is a prefix of \(\delta\) continue searching at node \(\overline{\alpha\beta}\). If you were able to find \(\delta\) in \(ST(S)\), \(S\) contains \(\delta\) at any position denoted by the indexes of leafs below your point of discovery.

Minimal unique substrings

\(\alpha\) is a minimal unique substring if and only if \(S\) contains \(\alpha\) exactly once and any prefix \(\beta\) of \(\alpha\) can be found at least two times in \(S\).

To find such a minimal unique substring walk through the tree to nodes \(\overline\alpha\) with a leaf-edge \(f\). A minimal unique substring is \(\alpha c\) with \(c\) is the first char of \(label(f)\), because its prefix \(\alpha\) isn’t unique (\(\overline\alpha\) has at least two leaving edges) and every extended version \(\alpha c \beta\) has a prefix that is also unique.

Maximal repeats

A maximal pair is a tuple \((p_1,p_2,l)\), so that \(S[p_1\dots p_1 + l - 1] = S[p_2\dots p_2 + l - 1]\), but \(S[p_1-1] \neq S[p_2-1]\) and \(S[p_1+l] \neq S[p_2+l]\). A maximal repeat is the string represented by such tuple. If \(\alpha\) is a maximal repeat there is a node \(\overline\alpha\) in \(ST(S)\). To find the maximal repeats do a DFS on the tree. Label each leaf with the left character of the suffix that it represents. For each internal node:

• If at least one child is labeled with c, then label it with c
• Else if its children’s labels are diverse, label with c.
• Else then all children have same label, copy it to current node.

Path labels to left-diverse nodes are maximal repeats.

Generalized suffix trees

An extension of suffix trees are generalized suffix trees. With it you can represent multiple words in one single tree. Of course you have to modify the tree, so that you know which leaf index corresponds to which word. Just a little bit more to store in the leafs ;) A generalized suffix tree is printed in figure 2 of page one.

Further applications

There are a lot of other applications for a suffix tree structure. For example finding palindromes, search for regular expressions, faster computing of the Levenshtein distance, data compression and so on…

Implementation

I’ve implemented a suffix tree in Java. The tree is constructed via WOTD and finds maximal repeats and minimal unique substrings. I also wanted pictures for this post, thus, I added a functionality that prints GraphViz code that represents the tree.