binfalse

Suffix trees are an application to particularly fast implement many important string operations like searching for a pattern or finding the longest common substring.

Introduction and definitions

I already introduced the Z-Algorithm which optimizes the searching for a pattern by preprocessing the pattern. It is very useful if you have to search for one single pattern in a large number of words. But often you’ll try to find many patterns in a single text. So the preprocessing of each pattern is ineffective. Suffix trees come up with a preprocessing of the text, to speed up the search for any pattern.

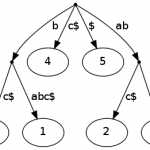
As expected a suffix tree of the word \(S\in\Sigma^+\) (length \(|S|=m\)) is represented in a data structure of a rooted tree. Every path from root to a leave represents a suffix of \(S\\)$ with \(\$\notin\Sigma\). The union \(\Sigma\cup\$=\tilde{\Sigma}\). Every inner node (except root) has at least two children. Every edge is labeled with a string of \(\tilde{\Sigma}^+\), labels of leaving edges at a single node start with different symbols and each leaf is indexed with \(1\dots m\). The concatenation of all edge labels on a path from root to a leaf with index \(i\) represents the suffix \(S[i\dots m]\).

Definition 1: For each node \(n\):

The path from root to \(n\) is called \(p\)

• The union of the labels at all edges on \(p\) is \(\alpha\in\tilde{\Sigma}^*\)
• \(\alpha\) is label of path \(p\) (\(\alpha=\text{label}(p)\))
• \(\alpha\) is path label to \(n\) (\(\alpha=\text{pathlabel}(n)\))
• instead of \(n\) we can call this node \(\overline \alpha\)

Definition 2: A pattern \(\alpha\in\Sigma^*\) exists in suffix tree of \(S\in\Sigma^+\) (further called \(ST(S)\)) if and only if there is a \(\beta\in\tilde{\Sigma}^*\), so that \(ST(S)\) contains a node \(n\) with \(\alpha\beta=\text{pathlabel}(n)\) (\(n=\overline{\alpha\beta}\)).

Definition 3: A substring \(\alpha\) ends in node \(\overline \alpha\) or in an edge to \(\overline{\alpha\beta}\) with \(\beta\in\tilde{\Sigma}^*\).

Definition 4: A edge to a leaf is called leaf-edge.

The tree \(ST(ababc)\) contains all suffixes of the word \(ababc\) extended with \(\\)$. This tree is visualized in figure 1.

Building suffix trees: Write only top down

The write-only, top-down (WOTD) algorithm constructs the suffix tree in a top-down fashion.

Algorithm

Let \(\overline \alpha\) be a node in \(ST(S)\), then \(\alpha\) denotes the concatenation of all edge labels on the path to \(\overline \alpha\) (\(\alpha=\text{pathlabel}(\overline \alpha)\)). Each node \(\overline \alpha\) in the suffix tree represents the set of all suffixes that have the prefix \(\alpha\). So the set of pathlabels to leafs below \(\overline \alpha\) can be written as \(R(\overline \alpha)=\{\beta|\beta \in \tilde{\Sigma}^* \wedge \alpha\beta \text{ is suffix of }S\}\) (all suffixes of the set of suffixes that start with \(\alpha\)).

This set is splitted in equivalence classes for each symbol \(c\) with \(G(\overline \alpha, c)=\{c\beta\|c\in \tilde{\Sigma}\wedge c\beta \in R(\overline \alpha)\}\) is the \(c\)-group of \(R(\overline \alpha)\).

Case 1: For groups \(G(\overline \alpha, c)\) that contain only one suffix \(\beta\) we create a leaf \(\overline{\alpha\beta}\) with the index \(|S| - |\alpha\beta|\) and connect it to \(\overline \alpha\) with an edge containing label \(\beta\). Case 2: In groups \(G(\overline \alpha, c)\) with a size of at least two we compute their longest common prefix \(\gamma\) that starts with \(c\) and create a node \(\overline{\alpha\gamma}\). The connecting edge between \(\overline \alpha\) and \(\overline{\alpha\gamma}\) gets the label \(\gamma\) and we continue recursively with this algorithm in node \(\overline{\alpha\gamma}\) with \(R(\overline{\alpha\gamma})=\{\beta|\beta \in \tilde{\Sigma}^* \wedge \alpha\gamma\beta \text{ is suffix of }S\}=\{\beta|\gamma\beta\in R(\overline \alpha)\}\)

Applications

Exact pattern matching

All paths from the root of the suffix tree are labeled with the prefixes of path labels. That is, they’re labeled with prefixes of suffixes of the string \(S\). Or, in other words, they’re labeled with substrings of \(S\). To search for a pattern \(\delta\) in \(S\), just go through \(ST(S)\), following paths labeled by the characters of \(\delta\). At any node \(\overline\alpha\) with \(\alpha\) is prefix of \(\delta\) find the edge with label \(\beta\) that starts with symbol \(\delta[|\alpha|+1]\). If such an edge doesn’t exists, \(\delta\) isn’t a substring of \(S\). Otherwise try to match the pattern with \(\beta\) to node \(\overline{\alpha\beta}\). If \(\alpha\beta\) is not a prefix of \(\delta\) you’ll either get a mismatch denoting that \(\delta\) isn’t a substring of \(S\), or you ran out of caracters of \(\delta\) and found it in the tree. If \(\alpha\beta\) is a prefix of \(\delta\) continue searching at node \(\overline{\alpha\beta}\). If you were able to find \(\delta\) in \(ST(S)\), \(S\) contains \(\delta\) at any position denoted by the indexes of leafs below your point of discovery.

Minimal unique substrings

\(\alpha\) is a minimal unique substring if and only if \(S\) contains \(\alpha\) exactly once and any prefix \(\beta\) of \(\alpha\) can be found at least two times in \(S\).

To find such a minimal unique substring walk through the tree to nodes \(\overline\alpha\) with a leaf-edge \(f\). A minimal unique substring is \(\alpha c\) with \(c\) is the first char of \(label(f)\), because its prefix \(\alpha\) isn’t unique (\(\overline\alpha\) has at least two leaving edges) and every extended version \(\alpha c \beta\) has a prefix that is also unique.

Maximal repeats

A maximal pair is a tuple \((p_1,p_2,l)\), so that \(S[p_1\dots p_1 + l - 1] = S[p_2\dots p_2 + l - 1]\), but \(S[p_1-1] \neq S[p_2-1]\) and \(S[p_1+l] \neq S[p_2+l]\). A maximal repeat is the string represented by such tuple. If \(\alpha\) is a maximal repeat there is a node \(\overline\alpha\) in \(ST(S)\). To find the maximal repeats do a DFS on the tree. Label each leaf with the left character of the suffix that it represents. For each internal node:

• If at least one child is labeled with c, then label it with c
• Else if its children’s labels are diverse, label with c.
• Else then all children have same label, copy it to current node.

Path labels to left-diverse nodes are maximal repeats.

Generalized suffix trees

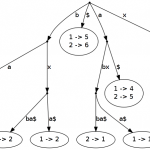
An extension of suffix trees are generalized suffix trees. With it you can represent multiple words in one single tree. Of course you have to modify the tree, so that you know which leaf index corresponds to which word. Just a little bit more to store in the leafs ;) A generalized suffix tree is printed in figure 2 of page one.

Further applications

There are a lot of other applications for a suffix tree structure. For example finding palindromes, search for regular expressions, faster computing of the Levenshtein distance, data compression and so on…

Implementation

I’ve implemented a suffix tree in Java. The tree is constructed via WOTD and finds maximal repeats and minimal unique substrings. I also wanted pictures for this post, thus, I added a functionality that prints GraphViz code that represents the tree.

Wow, the new kernel is the 100^th.

~ % grep '^kernel' /boot/grub/menu.lst | wc -l
100

(That was the reason why the dist-upgrade took more than an hour!^^)

I just dist-upgraded to aptosid, sidux is gone.

Yesterday the sidux team announced that sidux is dead, but the good news just followed:

As I am sure you are all aware, there have been interesting times for sidux recently. The bad news is that the sidux project is dead. The good news is that aptosid has been aptly born like a phoenix from the ashes and will provide a smooth upgrade for sidux systems. In many ways nothing has changed but our name.

After a long period of silence I already change the OS on my notebook from sidux to grml. It’s a very good alternative, but I decided to wait for an official announcement before deleting my main OS.

Now, the official announce is released, I upgraded my system to aptosid. First of all I created a aptosid.list in my /etc/apt/sources.list.d/ containing:

deb http://debian.tu-bs.de/project/aptosid/debian/ sid main fix.main contrib fix.contrib non-free fix.non-free vdr
deb-src http://debian.tu-bs.de/project/aptosid/debian/ sid main fix.main contrib fix.contrib non-free fix.non-free vdr

deb ftp://ftp.spline.de/pub/aptosid/debian/ sid main fix.main contrib fix.contrib non-free fix.non-free vdr
deb-src ftp://ftp.spline.de/pub/aptosid/debian/ sid main fix.main contrib fix.contrib non-free fix.non-free vdr

After wards calling aptitude update to reread the package listings. It notifies me that the new servers couldn’t be verified, I had to install the new keyring:

aptitude install aptosid-archive-keyring

It’s time to upgrade:

aptitude update
aptitude dist-upgrade

That fails at the first time:

Running update-initramfs.
update-initramfs: Generating /boot/initrd.img-2.6.35-4.slh.9-aptosid-amd64
initrd.img(/boot/initrd.img-2.6.35-4.slh.9-aptosid-amd64
) points to /boot/initrd.img-2.6.35-4.slh.9-aptosid-amd64
 (/boot/initrd.img-2.6.35-4.slh.9-aptosid-amd64) -- doing nothing at /var/lib/dpkg/info/linux-image-2.6.35-4.slh.9-aptosid-amd64.postinst line 348.
vmlinuz(/boot/vmlinuz-2.6.35-4.slh.9-aptosid-amd64
) points to /boot/vmlinuz-2.6.35-4.slh.9-aptosid-amd64
 (/boot/vmlinuz-2.6.35-4.slh.9-aptosid-amd64) -- doing nothing at /var/lib/dpkg/info/linux-image-2.6.35-4.slh.9-aptosid-amd64.postinst line 348.
Running /usr/sbin/update-grub.
Can't exec "/usr/sbin/update-grub": No such file or directory at /var/lib/dpkg/info/linux-image-2.6.35-4.slh.9-aptosid-amd64.postinst line 770.
User postinst hook script [/usr/sbin/update-grub] failed to execute: No such file or directory
dpkg: error processing linux-image-2.6.35-4.slh.9-aptosid-amd64 (--configure):
 subprocess installed post-installation script returned error exit status 255

As you see, /usr/sbin/update-grub wasn’t found. It is in grub-pc , but I have no idea why there isn’t a dependency so that grub-pc is installed by default!? Not fine but doesn’t matter, just install it:

aptitude install grub-pc
aptitude dist-upgrade

If this is done, just reboot and join the new kernel version 2.6.35 (slh is the greatest!!).

~ % uname -r
2.6.35-4.slh.9-aptosid-amd64

This evening I implemented a XMPP bridge to twitter. So I’ll get all news via IM and can update my status by sending an IM to a bot.

Nothing new, I don’t like the twitter web interface. Neither to read, nor to write messages. So I developed some scripts to tweet from command line. These tools are still working, but not that comfortable as preferred.

Today I had a great thought. At Gajim I’m online at least 24/7, talking with people, getting news etc. So the comparison with twitter is obvious.

After some research how to connect to twitter and jabber I decided to implement the bot in Perl. I still worked a little bit with Net::Twitter, so one side of the connection is almost done. For the other side I used the module Net::Jabber::Bot to implement a bot listening for messages or commands and sending twitter news via IM to my jabber account. The call for the jabber bot looks like:

my $bot = Net::Jabber::Bot->new ({
	server => $j_serv
	, port => $j_port
	, username => $j_user
	, password => $j_pass
	, alias => $j_user
	, message_function => \\&messageCheck
	, background_function => \\&updateCheck
	, loop_sleep_time => 40
	, process_timeout => 5
	, forums_and_responses => {}
	, ignore_server_messages => 1
	, ignore_self_messages => 1
	, out_messages_per_second => 20
	, max_message_size => 1000
	, max_messages_per_hour => 1000});

$bot->SendPersonalMessage($j_auth_user, "hey i'm back again!");
$bot->Start();

Most of it should be clear, the function messageCheck is called when a new message arrives the bot’s jabber account. There I parse the text whether it starts with ! (then it’s a command) otherwise the bot schould take the message to update the twitter status. updateCheck is the background function, it’s called when the bot idles. Here is time to check for news at twitter. It is called loop_sleep_time secs.

The rest is merely a matter of form. News from twitter are jabber’ed, IM’s from the authorized user are twitter’ed. Cool, isn’t it!?

Just download the tool, create a new jabber account for the bot (you’ll get one for example from jabber.ccc.de) and update the jmt.conf file with your credentials. Of course you need the additional Perl modules, if you also experience various problems with Net::Jabber::Bot try to use the latest code from git://github.com/toddr/perl-net-jabber-bot.git.

The bot could simply be launched by running the Perl script. Send !help to the bot to get some information about known commands. Just start it at any server/PC that has a network connection.

What comes next? If anyone would provide a server I would like to implement a multiuser tool, maybe with database connectivity!?

I’m actually learning some stuff related to algorithms on sequences. The naive search for a pattern in a long string is of course very slow and comes with a lot of unintelligent compares. The Z-Algorithm improves the searching by preprocessing the pattern.

Naive searching

A simple search algorithm written in java may look like

public void search (String needle, String haystack)
{
	for (int off = 0; off < haystack.length () - needle.length () + 1; off++)
	{
		boolean found = true;
		for (int p = 0; p < needle.length (); p++)
			if (needle.charAt (p) != haystack.charAt (off + p))
			{
				found = false;
				break;
			}
		if (found) System.out.println ("Fount pattern at position " + off);
	}
}

This code reliably finds any existence of needle in haystack in \(O(m \cdot n)\), with \(m=\) length of needle and \(n=\) length of haystack. That screams for improvements ;)

Definitions

The first algorithm that I want to present in this series is called Z-Algorithm. First of all we need some definitions.

Definition 1: In the following we denote \(S[i\dots j]\) as the substring of \(S\) beginning at position \(i\) and ending at position \(j\). We can also leave one of the limits clear, so that \(S[i\dots]\) is the substring \(S[i\dots |S|]\) and \(S[\dots j]\) means \(S[1\dots j]\).

Definition 2: \(Z_i(S) := \max \{p | S[i \dots i+p-1] = S[1 \dots p]\}\) So \(Z_i(S)\) is the length of the longest prefix of the suffix \(S[i\dots]\) that is also prefix of \(S\) itself. To abbreviate \(Z_i(S)\) is further on mentioned as \(Z_i\).

Definition 3: The set \([i,i+Z_i-1]\) for a \(Z_i > 0\) is called Z-Box at position \(i\).

Definition 4: \(V_i := \{[a_j, b_j] | [a_j, b_j] \text{ is Z-Box at } a_j \wedge a_j < i\}\) \(V_i\) is the set of limits of all Z-Box’es that start at the left-handed side of \(i\). Consider \(i<j \Rightarrow V_i \subseteq V_j\).

Definition 5: \([l_i,r_i] := \begin{cases} \underset{b_j}{\arg\max} \ [a_j,b_j] \in V_i, & \text{if } V_i \ne \varnothing\\ [0,0] & \text{else}\end{cases}\) If \(l_i>0\) and \(r_i>0\), \([l_i,r_i]\) defines the rightest Z-Box that starts before respectively at position \(i\). Consider \(i<j \Rightarrow r_i\le r_j\).

Algorithm

In the following \(i\) will denote the actual position we are looking for, \(l\) and \(r\) describe the current respectively last found of a Z-Box. First of all we set the values \(l\) and \(r\) to zero because we haven’t found any Z-Box yet. \(Z_2\) of our text \(S\) is according to Definition 2 the length of the longest prefix of \(S[2\dots]\) that is also prefix of \(S\) itself. If \(Z_2>0\) we found a first Z-Box and update the limits to \(l=2\) and \(r=2+Z_2-1\).

Now we have to run through the word \(S\), so \(i=3\dots \|S\|\) with \(\|S\|\) defines the length of \(S\).

Case 1: Let’s assume position \(i\) is outside of the last found Z-Box or we didn’t find any Z-Box yet (\(i>r\)). We find \(Z_i\) by comparing the prefixes of \(S\) and \(S[i\dots]\). If \(Z_i>0\) we’ve found a new Z-Box and need to update the limits to \(l=i\) and \(r=i+Z_i-1\).

Case 2: If the current position \(i\) is inside of a current Z-Box (\(i\le r\)) we try to find the equivalent position at the beginning of \(S\). The position we are searching for is \(k=i-l+1\) steps off the beginning of \(S\) (we are \(i-l+1\) steps behind \(l\) and \(S[l\dots]\) has the same prefix as \(S\)). Case 2a: If we don’t break out of the current Z-Box by creating another Z-Box with the length of the box at position \(k\) (\(Z_k<r-i+1\), so position \(i+Z_k\) is not behind position \(r\)), we can simply apply this Z-Box to the current position and \(Z_i=Z_k\). Case 2b: Otherwise, if we would leave the actual Z-Box (\(i + Z_k>r\)) we have to recheck the prefix conditions of \(S[i\dots]\) and \(S\). We know that \(S[i\dots r]\) equals \(S[1\dots r-i+1]\), so we only have to find the length of the longest prefix \(p\) of \(S[r-i+2\dots]\) that equals the prefix of \(S[r+1\dots]\). Now we can apply the new Z-Box such that \(Z_i=r-i+1+p\) and of course we update the Z-Box limits to \(l=i\) and \(r=i+Z_i-1\).

If we reached the end of \(S\) all Z-Boxes are found in \(\Theta(\|S\|)\).

Pseudo code

l = r = 0
Z[2] = prefix (S, S[2 ..]).length
if Z[2] > 0 then
	l = 2
	r = 2 + Z[2] - 1

for i = 3..|S| do
	if i > r then 										'(case 1)'
		Z[i] = prefix (S, S[i ..]).length
		if Z[i] > 0 then
			l = i
			r = i + Z[i] - 1

	else 												'(case 2)'
		k = i - l + 1
		if Z[k] < r - i + 1 then 						'(case 2a)'
			Z[i] = Z[k]

		else											'(case 2b)'
			p = prefix (S[r - i + 2 ..], S[r + 1 ..]).length
			Z[i] = r - i + 1 + p
			l = i
			r = i + Z[i] - 1

Example

Let me demonstrate the algorithm with a small example. Let’s take the word \(S=aabaaab\). First we start with \(l=0\) and \(r=0\) at position 2. \(Z_2\) is the length of the shared prefix of \(S\) (\(aabaaab\)) and \(S[2\dots]\) (\(abaaab\)). Easy to see the prefix is \(a\) with a length of 1. So \(Z_2=1\), \(l=2\) and \(r=2\). At the beginning of our for-loop the program’s status is:

At the first round in the loop \(i=3\), so \(i>r\) because \(r=2\). So we meet case 1 and have to find the length of the prefix of \(S\) (\(aabaaab\)) and \(S[3\dots]\) (\(baaab\)). Of course it’s zero, nothing to do.

Next round, we’re at position 4 and again \(i>r\) (case 1). So we have to compare \(aabaaab\) and \(aaab\). The longest prefix of both words is \(aa\) with a length of 2. So we start a new Z-Box at 4 with a size of 2, so \(l=4\) and \(r=5\).

With \(i=5\) and \(r=5\) we reach case 2 for the first time. \(k=i-l+1=2\) so our similar position at the beginning of \(S\) is position 2. \(Z_2=1\) and \(r-i+1=1\) so we are in case 2b and have to find the shared prefix of \(S[2 ..]\) (\(abaaab\)) and \(S[6 ..]\) (\(ab\)). It’s \(ab\), so \(p=2\) and \(Z_5=r-i+1+p=3\). \(l=5\) and \(r=7\).

Next round brings us \(i=6<r\), therefor we’re in case 2. Equivalent position is again \(k=i-l+1=2\), but now \(Z_2=1<r-i+1=2\) and we’re in case 2a and can just set \(Z_6=1\).

The last round we have to process is \(i=7<r\), case 2. Equivalent position is \(k=i-l+1=3\) and \(Z_3=0<r-i+1=1\), so case 2a and \(Z_7 = 0\).

That’s it. The Z-Box’es we’ve found are visualized in the image.

Searching

To search for a pattern \(P \in A^*\) in a text \(T \in A^*\) just calculate the Z-Boxes of \(P\$T\) with \(\$\notin A\). These calculations are done in \(\Theta(|T|)\). For any \(i>|P|\): If \(Z_i=|P|\) means \(P\$T[i\dots i+|P|-1]\) is prefix of \(P\$T\), so \(P\) is found at position \(i-(|P|+1)\) in \(T\).

Code

Of course I’m providing an implementation, see attachment.