binfalse

Just sitting around with Micha on a SunRay (maybe meanwhile OracleRay?). He is surfing through the web until his session seems to hang and he said:

Fuck FLASH!! Need the flash-trick...

I didn’t heard about that trick before, but now he told me that feature.

If Flash kills your SunRay session you have to type Ctrl+Alt+Moon , relogin and your session will revive. With running Flash!

As far as I know this happens very often when he is using his browser because unfortunately the whole web is contaminated with this fucking Flash… The Flash-Trick is very nice, but a flashblock plugin would be more user friendly!?

My boss wants to present some cool things in a lecture that can be done with SUN Spots. I'm selected to program these things and now I have three of them to play a little bit.

The installation was basically very easy, all you should know is that there is no chance for 64bit hosts and also Virtual Box guests don't work as expected, virtual machines lose the connection to the Spot very often... So I had to install a 32bit architecture on my host machine (btw. my decision was a Sidux Μόρος).

If a valid system is found, the rest is simple. Just download the SPOTManager from sunspotworld.com, that helps you installing the Sun SPOT Software Development Kit (SDK). If it is done connect a Sport via USB, open the SPOTManager and upgrade the Spot's software (it has to be the same version as installed on your host). All important management tasks can be done with this tool and it is possible to create virtual Spots.

Additionally to the SDK you'll get some demos installed, interesting and helpful to see how things work. In these directories ant is configured to do that crazy things that can be done with the managing tool. Here are some key targets:

ant info		# get some info about the spot (version, installed application and so on)
ant deploy		# build and install to spot
ant host-run	# build a host application and launch it
ant help		# show info about existing targets
# to configure a spot to run as base station OTA has to be disabled and basestation must be started
ant disableota startbasestation

A basestation is able to administrate other Spots, so you don't have to connect each to your machine.

Ok, how to do own stuff?
There are some Netbeans plugins that makes live easier, but I don't like that big IDE's that are very slow and bring a lot of overhead to your system. To create an IDE independent project that should run on a Spot you need an environment containing:

• File: ./resources/META-INF/MANIFEST.MF

  MIDlet-Name: NAME
  MIDlet-Version: 1.0.0
  MIDlet-Vendor: Sun Microsystems Inc
  MIDlet-1: App Description, ,your.package.MainClassName
  MicroEdition-Profile: IMP-1.0
  MicroEdition-Configuration: CLDC-1.1

• File: ./build.xml

  < ?xml version="1.0" encoding="UTF-8" standalone="no"?>
  <project basedir="." default="deploy">
  <property file="${user.home}/.sunspot.properties"/>
      <import file="${sunspot.home}/build.xml"/>
  </project>

• Directory: ./src
  Here you can place your source files

And now you can just type `ant` and the project will be deployed to the Spot.
A project that should run on your host communicating with other spots through the basestation needs a different environment:

• File: ./build.xml

  < ?xml version="1.0" encoding="UTF-8" standalone="no"?>
  <project basedir="." default="host-run">
  <property name="main.class" value="your.package.MainClassName"/>
  <property file="${user.home}/.sunspot.properties"/>
      <import file="${sunspot.home}/build.xml"/>
  </project>

• Directory: ./src
  Here you can place your source files

Ok, that's it for the moment. I'll report results.

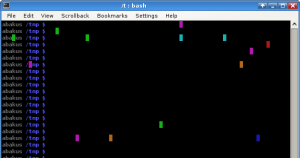
About one month ago, it was April 1^st, I attached two more lines to the .bashrc of Rumpel (he is co-worker and has to operate that day).

These two lines you can see here:

# kleiner april-scherz von dein freund martin :P
export PROMPT_COMMAND='if [ $RANDOM -le 32000 ]; then printf "\\0337\\033[%d;%dH\\033[4%dm \\033[m\\0338" $((RANDOM%LINES+1)) $((RANDOM%COLUMNS+1)) $((RANDOM%8)); fi'

With each appearance of the bash prompt this command paints one pixel in the console with a random color. No respect to important content beyond this painting. That can really be annoying and he was always wondering why this happens! For more than one month, until now!

Today I lift the secret, so Rumpel, I’m very sorry ;)

I just wanted to split a video file in each single frame and did not find a program that solves this problem. A colleague recommended videodub, but when I see DLL’s or a .exe I get insane! I’ve been working a little bit with OpenCV before and coded my own solution, containing only a few lines.

The heart of my solution consists of the following 13 lines:

CvCapture *capture = cvCaptureFromAVI(video.c_str());
if (capture)
{
	IplImage* frame;
	while (frame = cvQueryFrame(capture))
	{
		stringstream file;
		file < < prefix << iteration << ".png";
		cvSaveImage(file.str ().c_str (), frame);
		iteration++;
	}
}
cvReleaseCapture( &capture );

It just queries each frame of the AVI and writes it to an image file. Thus, not a big deal.

The complete code can be downloaded here. All you need is OpenCV and a C++ compiler:

g++ -I /usr/local/include/opencv -lhighgui -o vidsplit.out vidsplit.cpp

Just start it with for example:

./vidsplit.out --input video.avi --prefix myframes_

If you prefer JPG images (or other types) just change the extension string form .png to .jpg .

In one of our current exercises we have to prove different properties belonging to distance matrices as base of binary trees. Additionally I tried to develop an algorithm for creating such a tree, given a distance matrix.

A distance matrix \(D \in \mathbb{R}^{N,N}\) represents the dissimilarity of \(N\) samples (for example genes), so that the number in the i-th row j-th column is the distance between element i and j. To generate a tree of it, it is necessary to determine some attributes of the distance \(d(x,y):\mathbb{R}^n \times \mathbb{R}^n \rightarrow \mathbb{R}\) between two elements so that it is a metric:

1. \(d(x, y) \ge 0\) (distances are positive)
2. \(d(x, y) = 0 \Leftrightarrow x = y\) (elements with distance 0 are identical, dissimilar elements have distances greater than 0)
3. \(d(x, y) = d(y, x)\) (symmetry)
4. \(d(x, z) \le d(x, y) + d(y, z)\) (triangle inequality)

Examples for valid metrics are the euclidean distance \(\sqrt{\sum_{i=1}^n (x_i-y_i)^2}\), or the manhattan distance \(\sum_{i=1}^n \|x_i-y_i\|\).

The following procedure is called hierarchical clustering, we try to combine single objects to cluster. At the beginning we start with \(N\) cluster, each of them containing only one element, the intersection of this set is empty and the union contains all elements that should be clustered.

The algorithm now searches for the smallest distance in \(D\) that is not 0 and merges the associated clusters to a new one containing all elements of both. After that step the distance matrix should be adjusted, because two elements are removed and a new one is added. The distances of the new cluster to all others can be computed with the following formula:

\(X, Y\) are two clusters that should be merged, \(R\) represents another cluster. The constants \(\alpha, \beta, \gamma, \delta\) depend on the cluster method to use, shown in table 1.

Here \(\|X\|\) denotes the number of elements in cluster \(X\).

The algorithm continues with searching for the smallest distance in the new distance matrix and will merge the next two similar elements until just one element is remaining.
Merging of two clusters in tree-view means the construction of a parent node with both clusters as children. The first clusters containing just one element are leafs, the last node is the root of the tree.

Small example

Let’s create a small example from the distance matrix containing 5 clusters, see table 2.

A and D are obviously the most similar elements in this matrix, so we merge them. To make the calculation easier we take the average linkage method to compute the new distances to other clusters:

\(d(B,[A+D]) = \frac{d(B, A) + d(B, D)}{2} = \frac{5 + 4}{2} = 4.5\)
\(d(C,[A+D]) = \frac{d(C, A) + d(C, D)}{2} = \frac{2 + 1.5}{2} = 1.75\)
\(d(E,[A+D]) = \frac{d(E, A) + d(E, D)}{2} = \frac{6 + 5}{2} = 5.5\)

With these values we are able to construct the new distance matrix of 4 remaining clusters, shown in table 3.

This matrix gives us the next candidates for clustring, B and E with a distance of 1.5.

\(d([A+D], [B+E]) = \frac{d([A+D], B) + d([A+D], E)}{2} = \frac{4.5 + 5.5}{2} = 5\)
\(d(C,[B+E]) = \frac{d(C, B) + d(C, E)}{2} = \frac{3 + 4}{2} = 3.5\)

With the appropriate distance matrix of table 4.

Easy to see, now we cluster [A+D] with C:

and obtain a last distance matrix with table 5.

Needless to say, further calculations are trivial. There are only to clusters left and the combination of them gives us the final cluster containing all elements and the root of the desired tree.
The final tree is shown in figure 1. You see, it is not that difficult as expected and ends in a beautiful image!

Remarks

If \(D\) is defined as above there is no guarantee that edge weights reflect correct distances! When you calculate the weights in my little example you’ll see what I mean. If this property is desired the distance function \(d(x,y)\) has to comply with the condition of ultrametric inequality: \(d(x, z) \le \max {d(x, y),d(y, z)}\).

The method described above is formally known as agglomerative clustering, merging smaller clusters to a bigger one. There is another procedure that splits bigger clusters into smaller ones, starting with a cluster that contains all samples. This method is called divisive clustering.