binfalse

In one of our current exercises we have to prove different properties belonging to distance matrices as base of binary trees. Additionally I tried to develop an algorithm for creating such a tree, given a distance matrix.

A distance matrix \(D \in \mathbb{R}^{N,N}\) represents the dissimilarity of \(N\) samples (for example genes), so that the number in the i-th row j-th column is the distance between element i and j. To generate a tree of it, it is necessary to determine some attributes of the distance \(d(x,y):\mathbb{R}^n \times \mathbb{R}^n \rightarrow \mathbb{R}\) between two elements so that it is a metric:

1. \(d(x, y) \ge 0\) (distances are positive)
2. \(d(x, y) = 0 \Leftrightarrow x = y\) (elements with distance 0 are identical, dissimilar elements have distances greater than 0)
3. \(d(x, y) = d(y, x)\) (symmetry)
4. \(d(x, z) \le d(x, y) + d(y, z)\) (triangle inequality)

Examples for valid metrics are the euclidean distance \(\sqrt{\sum_{i=1}^n (x_i-y_i)^2}\), or the manhattan distance \(\sum_{i=1}^n \|x_i-y_i\|\).

The following procedure is called hierarchical clustering, we try to combine single objects to cluster. At the beginning we start with \(N\) cluster, each of them containing only one element, the intersection of this set is empty and the union contains all elements that should be clustered.

The algorithm now searches for the smallest distance in \(D\) that is not 0 and merges the associated clusters to a new one containing all elements of both. After that step the distance matrix should be adjusted, because two elements are removed and a new one is added. The distances of the new cluster to all others can be computed with the following formula:

\(X, Y\) are two clusters that should be merged, \(R\) represents another cluster. The constants \(\alpha, \beta, \gamma, \delta\) depend on the cluster method to use, shown in table 1.

Here \(\|X\|\) denotes the number of elements in cluster \(X\).

The algorithm continues with searching for the smallest distance in the new distance matrix and will merge the next two similar elements until just one element is remaining.
Merging of two clusters in tree-view means the construction of a parent node with both clusters as children. The first clusters containing just one element are leafs, the last node is the root of the tree.

Small example

Let’s create a small example from the distance matrix containing 5 clusters, see table 2.

A and D are obviously the most similar elements in this matrix, so we merge them. To make the calculation easier we take the average linkage method to compute the new distances to other clusters:

\(d(B,[A+D]) = \frac{d(B, A) + d(B, D)}{2} = \frac{5 + 4}{2} = 4.5\)
\(d(C,[A+D]) = \frac{d(C, A) + d(C, D)}{2} = \frac{2 + 1.5}{2} = 1.75\)
\(d(E,[A+D]) = \frac{d(E, A) + d(E, D)}{2} = \frac{6 + 5}{2} = 5.5\)

With these values we are able to construct the new distance matrix of 4 remaining clusters, shown in table 3.

This matrix gives us the next candidates for clustring, B and E with a distance of 1.5.

\(d([A+D], [B+E]) = \frac{d([A+D], B) + d([A+D], E)}{2} = \frac{4.5 + 5.5}{2} = 5\)
\(d(C,[B+E]) = \frac{d(C, B) + d(C, E)}{2} = \frac{3 + 4}{2} = 3.5\)

With the appropriate distance matrix of table 4.

Easy to see, now we cluster [A+D] with C:

and obtain a last distance matrix with table 5.

Needless to say, further calculations are trivial. There are only to clusters left and the combination of them gives us the final cluster containing all elements and the root of the desired tree.
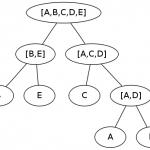
The final tree is shown in figure 1. You see, it is not that difficult as expected and ends in a beautiful image!

Remarks

If \(D\) is defined as above there is no guarantee that edge weights reflect correct distances! When you calculate the weights in my little example you’ll see what I mean. If this property is desired the distance function \(d(x,y)\) has to comply with the condition of ultrametric inequality: \(d(x, z) \le \max {d(x, y),d(y, z)}\).

The method described above is formally known as agglomerative clustering, merging smaller clusters to a bigger one. There is another procedure that splits bigger clusters into smaller ones, starting with a cluster that contains all samples. This method is called divisive clustering.

Neither hallucinations nor does anybody drugged your coffee, what you see is real!

I leave my old self-made blog and move to the content management system Wordpress due to various reasons. My schedule doesn’t allow profound modification to get some important features that Wordpress gives me for free. Behind this solution a lot of developer are working on this open source project and there are a huge bunch of plugins and for probably any problem Wordpress and its plugin developers offers a solution.

The layout is chosen to be simple and clear, just like my previous blog, and important: It is valid! Maybe by the time I’ll port some of the older entries to this new blog, to get them listed between search results.

There is on additional improvement. I’ll try to overcome my inner pigdog lack of will power and compose some articles in English. I hope it will tweak my language abilities. If you find some mistakes, please correct me!

So, lets start!

Some content isn’t available for every one, e.g. our frontends for administration at the university are only accessible with special IP’s. A similar problem is the download of scientific paper from platforms like PubMed or Oxford Journals. Our university subscribed to these journals, but unless there is a SSO like Shibboleth they are just available from inside the university network. If I want to download such a publication from home I need to pay about US$30 or have to go to an university computer and get it there because there is no proxy available at our university. But there must be workaround to surf with an university IP from home!

And it is! All you need is an account for an *nix system at your company/library/university or whatever! Just create a SSH tunnel to it:

ssh -D8080 USER@SERVER.WITH.PREFFERED.IP

-D8080 defines the entrance point of the tunnel, in this example it is port 8080. Every other port (that is not yet in use) is possible, but remember that you need to be root to use ports below 1024. Now a SOCKS5 proxy is emulated by SSH. This SOCKS proxy will routes network packages from your localhost to a server through SERVER.WITH.PREFFERED.IP . To apply it just configure your browser to use the proxy at localhost:8080 and check your IP address at any service like this one.

But it’s a lot to do for just downloading a simple PDF, isn’t it? That need improvements!

The main work is to configuring the browser, for example Firefox needs 6 clicks and some keyboard inputs. That’s nasty, but there is a add-on called Foxy Proxy that manages different proxy settings through an icon on the status bar of Firefox. It’s also able to use SOCKS proxies and you can define regex-lists to use different proxys for special URL’s. This speeds up the switching between different proxies. For other browsers you might find similar solutions.

To optimize the creation of the tunnel you can first prepare SSH-keys without a passphrase and create a script containing:

#!/bin/bash

while true
do
    ssh -o ServerAliveInterval=60 -N -D8080 USER@SERVER
done

This script will create the tunnel (hence the SOCKS proxy) when it’s executed. So if you want a permanent tunnel you can call it from your $HOME/.loginrc or any other file that is executed when you login. Alternatively you can write a start-script…

This is a translation of my German entry.

Until now I managed my code/work with Subversion and all was very well, but I decided to move to a distributed revision control system. Calling spade as a spade my choice was Git.

After some tests I had the problem, that there is (basically) no central repository where everyone can commit changes, but I’m working with other guys on homework/projects. So how to centralize a distributed revision control system? Nothing easier than that!

Server set up

Software of choice is called gitosis, so install the following:

aptitude install git git-core gitosis

Gitosis will manage repositories and privileges on the repository server. The installation progress will add a new user to your system called gitosis (see /etc/passwd ). To initialize the master repository that will manage the rest just copy the SSH public key of your local account to /tmp/id_rsa.pub and do the following:

binfalse /home # su - gitosis
gitosis@binfalse:~$ gitosis-init < /tmp/id_rsa.pub
Initialized empty Git repository in /home/git/repositories/gitosis-admin.git/
Reinitialized existing Git repository in /home/git/repositories/gitosis-admin.git/
gitosis@binfalse:~$ exit

That’s it on the server, now you have a head-repository and you can manage everything on your local machine.

Managing the manage-repository

Right back on your local machine you also have to install Git:

aptitude install git git-core

Now you’re able to check out the previous created managing repository that knows your SSH key:

esmz-designz@abakus ~ $ mkdir git
esmz-designz@abakus ~ $ cd git/
esmz-designz@abakus ~/git $ git clone gitosis@HOST:gitosis-admin.git
Initialized empty Git repository in /home/esmz-designz/git/gitosis-admin/.git/
remote: Counting objects: 5, done.
remote: Compressing objects: 100% (4/4), done.
remote: Total 5 (delta 1), reused 5 (delta 1)
Receiving objects: 100% (5/5), done.
Resolving deltas: 100% (1/1), done.
esmz-designz@abakus ~/git $ l
total 12K
drwxr-xr-x 3 esmz-designz 4.0K 2009-08-23 01:19 ./
drwxr-xr-x 21 esmz-designz 4.0K 2009-08-23 01:14 ../
drwxr-xr-x 4 esmz-designz 4.0K 2009-08-23 01:19 gitosis-admin/
esmz-designz@abakus ~/git $ cd gitosis-admin/
esmz-designz@abakus ~/git/gitosis-admin $ l
total 20K
drwxr-xr-x 4 esmz-designz 4.0K 2009-08-23 01:19 ./
drwxr-xr-x 3 esmz-designz 4.0K 2009-08-23 01:19 ../
drwxr-xr-x 8 esmz-designz 4.0K 2009-08-23 01:19 .git/
-rw-r--r-- 1 esmz-designz 89 2009-08-23 01:19 gitosis.conf
drwxr-xr-x 2 esmz-designz 4.0K 2009-08-23 01:19 keydir/

The directory keydir holds known SSH keys from users that will work with you, gitosis.conf is the managing file. It is nearly empty on creation and may look like this:

[gitosis]

[group gitosis-admin]
writable = gitosis-admin
members = esmz-designz@abakus

To add a new repository just type something like this:

[repo RepositoryName]
owner = you@yourhost
description = some description words

And to create a new group of users:

[group GroupName]
writable = RepoTheyCanWrite1 RepoTheyCanWrite2
readonly = RepoTheyCanRead1 RepoTheyCanRead2
members = user1@host1 user2@host2

New users should give you their public key, so you can save it in the keydir directory with a name like user@host.pub . To commit the changes you’ve made type the following:

esmz-designz@abakus ~/git/gitosis-admin $ git commit -a
[master 51cdf92] Created repository test.
1 files changed, 4 insertions(+), 0 deletions(-)
esmz-designz@abakus ~/git/gitosis-admin $ git push

Now everybody that was enabled is allowed to checkout your projects. To initiate a new project you can do the following:

esmz-designz@abakus ~/git/gitosis-admin $ cd ..
esmz-designz@abakus ~/git $ mkdir test
esmz-designz@abakus ~/git $ cd test/
esmz-designz@abakus ~/git/test $ git init
Initialized empty Git repository in /home/esmz-designz/git/test/.git/
esmz-designz@abakus ~/git/test $ git remote add origin gitosis@HOST:test.git

To commit a first file:

esmz-designz@abakus ~/git/test $ echo "Usain Bolt" > WM_BERLIN
esmz-designz@abakus ~/git/test $ git add WM_BERLIN
esmz-designz@abakus ~/git/test $ git commit -m "Start der ersten Revision"
[master (root-commit) 444915d] Start der ersten Revision
1 files changed, 1 insertions(+), 0 deletions(-)
create mode 100644 WM_BERLIN
esmz-designz@abakus ~/git/test $ git push origin master:refs/heads/master
Initialized empty Git repository in /home/git/repositories/test.git/
Counting objects: 3, done.
Writing objects: 100% (3/3), 245 bytes, done.
Total 3 (delta 0), reused 0 (delta 0)
To gitosis@HOST:test.git
* [new branch] master -> master
esmz-designz@abakus ~/git/test $

Voila, there is your repository! Check it out, change it, branch it, you know what to do!

Publish a repository

With this configuration only you and a bunch of people can see what you are doing in your spare time, but what if you want to publish you work? You can create a git daemon that listens on port 9418 of your server, waiting for a user who wants clone your code:

binfalse /home # sudo -u gitosis git-daemon --base-path=$GITOSISHOME/repositories --verbose --detach
binfalse /home # ps -ef | grep git
gitosis 3216 1 0 00:57 ? 00:00:00 git-daemon --base-path=$GITOSISHOME/repositories/ --verbose --detach
binfalse /home #

This service will serve any repository content if you create a file called $REPOSITORYHOME/git-daemon-export-ok in this repository (content isn’t necessary). Everybody knows that such a daemon tends to die sometimes, so I created a cronjob:

*/5 * * * * [ -z `pidof git-daemon` ] && sudo -u gitosis git-daemon --base-path=$GITOSISHOME/repositories/ --verbose --detach

Now everybody can clone repositories with that special file that allows public cloning by:

git clone git://HOST/REPOSITORY.git

That’s it! not that difficult but one has to know what to do! Have fun with your repository.

This is a translation of my German article.

SSH is a secure way to connect to a remote system, e.g. for administration or remote working. The communication between these two workstations is encrypted, so an enemy is not able to intercept/spy on the transferred data.

Although the password that is sent to access the other system is encrypted, it’s still possible to brute force it. To decrease this risk one can turn off password authentication and just allow the authentication via SSH keys, so that the access is only possible for people that have a specific private keys. It is much harder to guess such a private key than guessing a password.

To create such a key pair, containing a private and a public key, just run ssh-keygen -t rsa -b 4096 in your terminal. This command will create an RSA-key width 4096 bits (the more bits the harder to guess the key). The output may look like this:

Generating public/private rsa key pair.
Enter file in which to save the key (/home/user/.ssh/id_rsa):
Created directory '/home/user/.ssh'.
Enter passphrase (empty for no passphrase):
Enter same passphrase again:
Your identification has been saved in /home/user/.ssh/id_rsa.
Your public key has been saved in /home/user/.ssh/id_rsa.pub.
The key fingerprint is:
16:59:cb:9f:55:b1:39:ee:b3:72:14:19:13:5c:60:4d user@abakus
The key's randomart image is:
+--[ RSA 4096]----+
|            . +*E|
|         + . . =+|
|          o o .++|
|     .  .    o.o.|
|           S o ..|
|         . ..    |
|        .o       |
|       .       .o|
|        o.       |
+-----------------+

Congratulations, your are now owner of a 4096 bit SSH-key! It is not necessary to assign a passphrase, so you can connect to the server without any password. But if anyone can get access to your private key he is also able to connect to any server that knows your public key! So it is very insecure and I recommend using a passphrase. For more options see man ssh-keygen.

If you now take a look in your $HOME/.ssh/ directory you’ll find two keys, a public key named id_rsa.pub and a private key id_rsa. This private key is just for you, don’t share it with anyone!

To publish the public key, you can use the ssh-copy-id tool:

user@abakus ~ $ ssh-copy-id user@192.168.0.111
The authenticity of host '192.168.0.111 (192.168.0.111)' can't be established.
RSA key fingerprint is 34:cd:e7:95:48:75:d4:16:86:84:19:f0:b4:d3:2c:ad.
Are you sure you want to continue connecting (yes/no)? yes
Warning: Permanently added '192.168.0.111' (RSA) to the list of known hosts.
user@192.168.0.111's password:
Now try logging into the machine, with "ssh 'user@192.168.0.111'", and check in:

.ssh/authorized_keys

to make sure we haven't added extra keys that you weren't expecting.

All that it does is appending the contents of your public key to the $HOME/.ssh/authorized_keys file of the user on the remote system (here remote is 192.168.0.111). If you don’t have the ssh-copy-id tool, you can do it manually but copying the contents of id_rsa.pub to the authorized_keys file of the remote user..

At the next login I don’t have to provide the password to the remote account, I only need the passphrase for the private key:

user@abakus ~ $ ssh user@192.168.0.111
Enter passphrase for key '/home/user/.ssh/id_rsa':
Linux siduxbox 2.6.30-4.slh.1-sidux-amd64 #1 SMP PREEMPT Sun Aug 2 09:58:18 UTC 2009 x86_64
Last login: Wed Aug 19 12:12:18 2009 from 192.168.0.55
user@siduxbox ~ $

If you didn’t supply a passphrase for the key you’ll never get asked for one.

Last but not least we can disable the password authentication with the following settings in /etc/ssh/sshd_config :

PasswordAuthentication no
UsePAM no

From now on, only people that have private keys, compatible to those public keys stored in $HOME/.ssh/authorized_keys on the server, can access the remote machine.